Kreise

26.1.2004

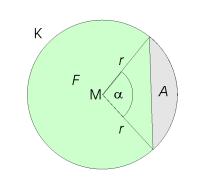
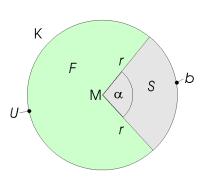
Sektor Der Kreis K um den Mittelpunkt M mit dem Radius r hat die Fläche und den Umfang . Das Verhältnis der Sektorfläche zur Gesamtfläche des Kreises ist ebenso wie das Verhältnis der Bogenlänge zum Kreisumfang gleich dem Verhältnis zwischen dem Öffnungswinkel und dem Winkel des Vollkreises (360° bzw. ):

zum Ende des Dokuments zum Abschnitt Segment Dieses Dokument als *.pdf downloaden

Daraus ergibt sich (mit in Grad)   bzw. (mit im Bogenmaß)  und (mit in Grad) bzw. (mit im Bogenmaß). Für die Umrechnung der Winkel gilt: bzw. .		<= Sektor eines Kreises
Segment
	Der Kreis K um den Mittelpunkt M mit dem Radius r hat die Fläche .  Die Fläche des Kreissegments (oder Kreisabschnitts) sei A, der Öffnungswinkel betrage .	zum Abschnitt Sektor

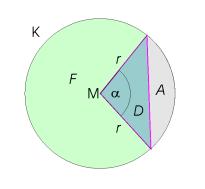
	Die Segmentfläche A unterscheidet sich von der Sektorfläche S (siehe oben) nur um ein gleichschenkliges Dreieck der Fläche D.
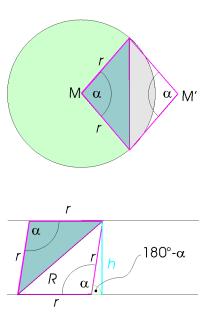
	Zur Berechnung von D spiegelt man das Dreieck an seiner Hypotenuse und erhält eine Raute der Fläche R. Die Fläche R der Raute ergibt sich aus mit zu . Dam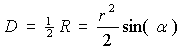it ist .
Die Segmentfläche A erhält man als Differenz der Sektorfläche S und der Dreiecksfläche D  zu (in Grad) bzw. (im Bogenmaß)		<= Segment eines Kreises

zum Abschnitt Sektor

zum Abschnitt Segment

zum Anfang des Dokuments

---