Das Ziegenproblem Ein Bauer besitzt eine Ziege und eine kreisförmige Wiese, auf der er diese Ziege weiden lassen möchte. Die Ziege wird mit einer Leine an einem senkrechten Pfahl festgebunden, der exakt auf dem Rand der Wiese steht. Welche Länge muss die Leine haben, damit die Ziege gerade die Hälfte der Fläche der kreisförmigen Wiese abgrasen kann? (Die Ziege und der Pfahl sind als punktförmig anzusehen.)

25.1.2004 zum Ende des Dokuments Dieses Dokument als *.pdf downloaden

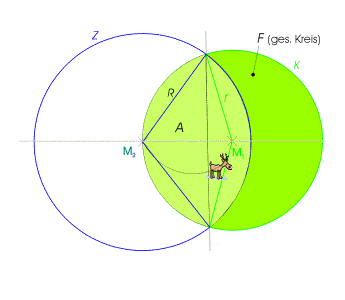
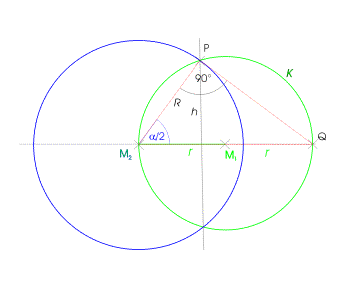
Die der Ziege zugängliche Fläche ist die Schnittfläche A zweier Kreise. Der Kreis K um M1 mit Radius r beschreibe die Wiese. Der Kreis Z um den Mittelpunkt M2 auf K beschreibt den Aktionsradius R der Ziege. R entspricht der gesuchten Länge der Leine. Die Fläche der Wiese (gesamter Kreis) beträgt . R muss so gewählt werden, dass gilt: .

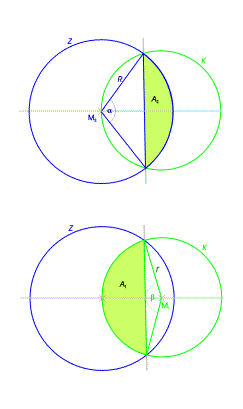
Die Schnittfläche A ergibt sich als Summe der beiden Teilflächen A1 und A2: A = A1 + A2. A1 ist ein Segment des Kreises K, A2 ein Segment des Kreises Z. Entsprechend der Formel zur Berechnung der Fläche von Kreissegmenten gilt: mit den jeweiligen Segmentwinkeln   und (im Bogenmaß!).
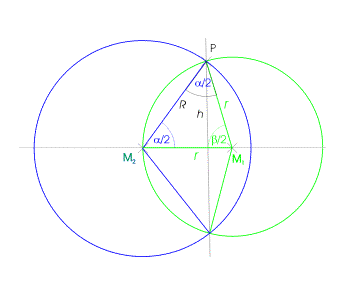
Die Winkel M1M2P und M2PM1 im gleichschenkligen Dreieck M2M1P mit den Seiten R, r und r sind gleich und betragen jeweils die Hälfte des Segmentwinkels   .   Daraus ergibt sich (Winkel in Grad) bzw. (Winkel im Bogenmaß). Somit ist und .

Vereinfachung mit Hilfe der bekannten Zusammenhänge zwischen den trigonometrischen Funktionen ergibt:

Das Dreieck M2QP ist rechtwinklig (K ist Thaleskreis über M2Q) mit der Hypotenuse 2r und der Ankathete R bzg. des Winkels   bei M2. Daraus folgt . Einsetzen in führt zu . Mit dem bekannten Zusammenhang (Formelsammlung) erhält man 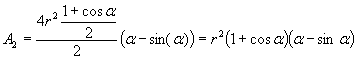bzw. .

Die Flächenbedingung lautet damit::

/ r²

Diese Gleichung ist meines Wissens nur näherungsweise lösbar. Interessant - aber bei genauerer Betrachtung einleuchtend  - ist die Tatsache, dass es für diese Gleichung eine eindeutige Lösung    gibt, die nicht vom Radius r der Wiese abhängt! Die Aufgabe ist also beliebig skalierbar. Ganz gleich, wie groß die Wiese ist, der Öffnungswinkel des Kreissegments A₂ ist konstant.

Wegen bedeutet das auch, dass die Länge R der Leine direkt proportional zum jeweiligen Radius r der Wiese ist::

Eine numerische Lösung

Nachfolgend ist die Funktion  gegen den Winkel 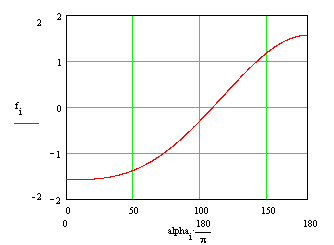  (in Grad) aufgetragen.

Der Detailausschnitt erlaubt das Ablesen der Nullstelle bei bzw. bei    (im Bogenmaß).

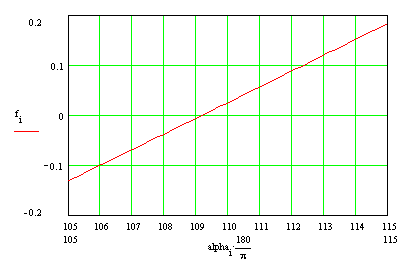
Mit folgt .
	zum Anfang des Dokuments

---